Методы частотного анализа
Существуют следующие базовые методы частотного анализа систем, которые могут быть реализованы в SimInTech:
- Частотный анализ линейных и линеаризованных систем методом расчета матрицы Якоби системы.
- Частотный анализ систем методом гармонического анализа при подаче на вход системы синусоидального сигнала.
- Спектральный анализ выходного сигнала системы методом подачи на вход системы шумоподобного или ступенчатого сигнала.
Частотный анализ линейных и линеаризованных систем методом расчета матрицы Якоби системы
Постановка задачи
- Экспериментальный расчет сводится к моделированию системы при гармоническом входном воздействии и последующему вычислению амплитуды и фазы выходного сигнала как первых коэффициентов разложения в ряд Фурье. Достоинство этого способа - возможность получать характеристики систем, содержащих сложные нелинейные элементы, недостатки - большой объем вычислительной работы и невозможность получить характеристики неустойчивых объектов.
- Алгебраический способ основан на формальной замене операторов дифференцирования, дискретизации и запаздывания соответствующими комплексными коэффициентами, зависящими от частоты, и решении полученной системы линейных алгебраических уравнений с комплексными коэффициентами. Этот способ требует меньших вычислительных затрат и позволяет получить характеристики неустойчивых объектов, но он применим только к линейным или предварительно линеаризованным моделям.
-
Метод передаточных функций удобно использовать в тех случаях, когда система полностью непрерывная и не содержит блоков чистого запаздывания либо полностью дискретная. В более сложных случаях данный метод почти не применяется ввиду необходимости формирования передаточной функции всей системы по передаточным функциям составляющей ее блоков, описывающих непрерывные элементы, запаздывания разной величины, а также дискретные элементы с различными периодами дискретизации. Один из способов решения этой проблемы - использование дробно-рациональной аппроксимации (аппроксимации Паде) экспоненциальной функции. Однако такой подход не всегда корректен, поскольку полученная аппроксимация порой оказывается недостаточно точной.
-
Метод переменных состояния иногда требует большей вычислительной работы при расчете характеристик непрерывных либо дискретных систем. Однако он более универсален и позволяет без труда рассчитывать частотные характеристики непрерывно-дискретных систем, содержащих блоки запаздывания и дискретные блоки с разными периодами дискретизации. Поэтому для реализации в SimInTech был выбран именно этот метод.
При расчете систем, содержащих дискретные элементы, необходимо иметь в виду, что экстраполятор, как правило, является нелинейным элементом. Однако, если рассматривать все функции времени как решетчатые функции, определенные только в моменты дискретизации, то экстраполятор становится линейным элементом. Если при этом моменты дискретизации всех дискретных элементов совпадают, то непрерывно-дискретную систему, не содержащую нелинейных функциональных зависимостей, рассматривают как линейную дискретную систему (необходимо только произвести дискретизацию непрерывной части системы, что приводит к расчету матричной экспоненты). Это является обоснованием применения преобразования Фурье для расчета систем, содержащих непрерывную и дискретную части. Однако такой подход неприменим в общем случае, когда система содержит дискретные элементы с различными периодами дискретизации.
Таким образом, будет использоваться подход, основанный на линеаризации экстраполятора. В непрерывном времени гармонически линеаризованную модель экстраполятора возможно представить в виде передаточной функции:
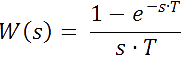
Поскольку при таком подходе передаточная функция экстраполятора не равна единице, то его последовательное включение приводит к изменению частотных характеристик. Поэтому следует четко определить, в каких случаях и в каких местах в схему должен быть включен экстраполятор. При моделировании функцию экстраполятора выполняет каждый дискретный блок, и его включение не обязательно. Включение экстраполятора с тем же периодом до или после дискретного блока никак не скажется на результатах моделирования. При частотном анализе экстраполятор с соответствующим периодом должен разделять непрерывную и дискретную части системы. При этом следует учитывать, что включение лишнего экстраполятора приведет к изменению результатов, поэтому следует ставить экстраполятор только на входе либо только на выходе дискретной части. В соответствии с этим правилом, если система полностью дискретная, то и нет разделения на дискретную и непрерывную части, поэтому включать экстраполятор в этом случае не следует.
Алгоритмы частотного анализа
При использовании метода переменных состояния расчет частотных характеристик сводится к выполнению следующих действий:
- Сформировать математическую модель в виде совместной системы дифференциальных, алгебраических и разностных уравнений.
- Линеаризовать полученные уравнения. При этом линеаризация будет происходить в окрестности заданной рабочей точки для дифференцирования в численном или аналитическом виде.
- Выполнить замену операторов дифференцирования, сдвига по времени и запаздывания на соответствующие комплексные коэффициенты усиления. В результате будет сформирована система линейных алгебраических уравнений с комплексными коэффициентами.
- Решив полученную систему, найти значения действительной Re(ω) и мнимой Im(ω) частей комплексной частотной характеристики.
- По значениям Re(ω), Im(ω) определить значения частотных характеристик.
Действия 3…5 выполняются для каждого из значений частоты, на которых рассчитываются частотные характеристики.
Более подробное описание каждого этапа расчета представлено ниже.
-
xdif - вектор переменных состояния дифференциальных уравнений;
- xalg - вектор определяющих алгебраических переменных (т.е. тех переменных, по которым однозначно определяются все переменные алгебраических контуров);
- xdis - вектор дискретных переменных состояния;
- xdel - вектор выходов блоков запаздывания;
-
xext - вектор выходов экстраполяторов.
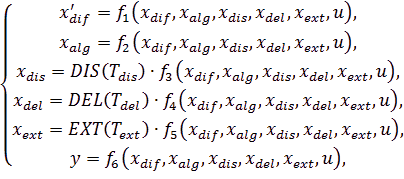
где DIS(Tdis) - оператор векторного покомпонентного дискретного запаздывания; Tdis - вектор соответствующих периодов дискретизации; DEL(Tdel), EXT(Text) - операторы покомпонентного запаздывания и экстраполяции; Tdel, Text - векторы соответствующих постоянных времени.
В SimInTech принято представление математической модели в виде структурной схемы, заданной уравнениями отдельных блоков и связями блоков между собой. В этом случае формирование уравнений в виде (*) обеспечивается процедурой сортировки блоков, включенной в SimInTech при реализации моделирования.
Линеаризация полученных уравнений сводится к определению матриц частных производных:
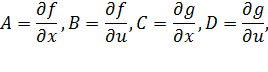
где f = [f1, f2, f3, f4, f5]T, x = [xdif, xalg, xdis, xdel, xext]T. Расчет этих матриц производиться численно, заменяя дифференциалы конечными приращениями. Алгоритм расчета матрицы A и вектора-строки C представлен ниже с использованием оператора языка Паскаль:
{ x0 - заданная рабочая точка }
f0 := f(x0, u);
g0 := g(x0, u);
for i := 1 to N do
begin
{ relinc - относительное приращение, absinc - абсолютное приращение }
dxi := relinc*abs(x[i]) + absink;
xsave := x0[i];
x0[i] := xsave + dxi;
f1 := f (x0, u);
g1 := g (x0, u);
for j := 1 to N do A[j, i] := ( f1[j] - f0[j] ) / dxi;
C[j] := (g1[j] - g0[j] ) / dxi;
x0[i] := xsave
end;Определение матриц B и D происходит аналогичным способом, путем задания приращения переменной u.
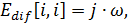
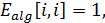
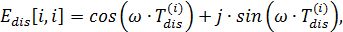
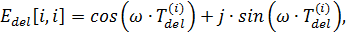
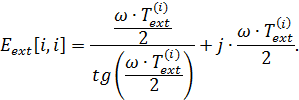
Принимая u = 1 и решая систему (*), требуется найти значения вещественной и мнимой частотных характеристик на заданной частоте ω: y = Re(ω) + jIm(ω).
Решение алгебраической системы с комплексными коэффициентами сводится к решению системы с вещественными коэффициентами, которая имеет вид:
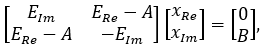
где EI, ER - действительная и мнимая части матрицы E. Тогда значения вещественной и мнимой характеристик определяются по формулам:
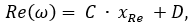
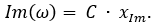
Значения амплитудной A(ω), логарифмической амплитудной L(ω) и фазовой j(ω) частотных характеристик вычисляются в виде:
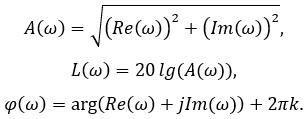
где arg - аргумент комплексного числа, который вычисляется по формуле:
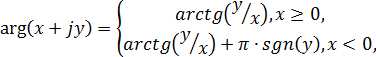
где k - целое число, задаваемое так, чтобы исключить разрывы фазовой характеристики.
Реализация в SimInTech
Примеры применения данной методики анализа систем приведены в примерах, расположенных в директории установки SimInTech: SimInTech\Demo\Графики и исследования\Частотный анализ
Однако данный метод ограничен возможными некорректными расчетами характеристик нелинейных систем, поскольку нелинейные элементы при малых приращениях не имеют возможности менять своего выхода (например, реле и прочие разрывные нелинейности) при недостаточной амплитуде приращений. Поэтому в разных траекториях системы метод выдает принципиально разные результаты (т.е., например, в один момент времени АЧХ будет нулевой, а в другой – ненулевой). Данный метод рекомендуется применять для частотного анализа линейных систем и для получения мгновенных частотных характеристик нелинейных систем. Кроме того, при этом методе затруднительно учесть влияние амплитуды входного сигнала на АЧХ системы (для нелинейных систем иногда принципиально).
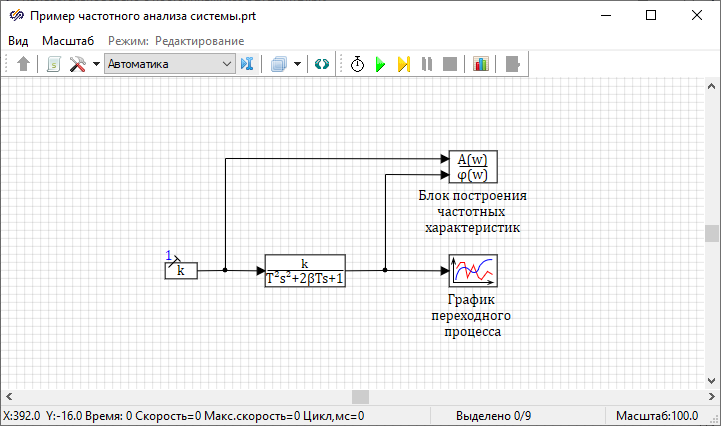
Для использования данного метода построения частотных характеристик в библиотеке присутствует блок Plotting of the frequency characteristics, который находится на вкладке «Анализ и оптимизация».
Для того, чтобы построить частотную характеристику с помощью данного блока, необходимо:
- Создать модель системы.
- Поместить на схему блок «Построение частотных характеристик».
- Первый вход этого блока подключить на выход блока, который установлен в качестве источника входного воздействия системы.
- Второй вход блока подключить на выход системы.
- Установить диапазон расчета частотных характеристик и их типы в свойствах блока (для этого необходимо выделить блок, вызвать контекстное меню нажатием на блок правой кнопкой мыши и в контекстном меню выбрать пункт «Свойства»).
- Нажать кнопку «Пуск» для расчета частотной характеристики системы и вывода ее на график.
Частотный анализ систем методом гармонического анализа при подаче на вход системы синусоидального испытательного сигнала
Алгоритм частотного анализа
На вход системы подается гармонический сигнал u(t) = a ⋅ sin(ωt). Установившийся сигнал на выходе системы возможно представить в виде суммы гармоник:
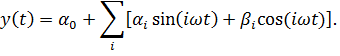
Тогда амплитуды и фазы гармоник рассчитываются по формулам:
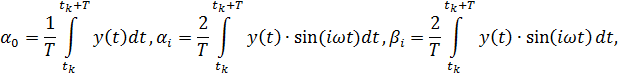
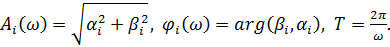
Значения частотной характеристики рассчитываются по 1-й гармонике:
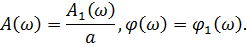
Интервал оценки АЧХ выбирается из расчета tk = kT, а значения характеристик оцениваются на каждом интервале [t1, t2], …, [tk, tk+1] до тех пор, пока разность оценок между соседними интервалами не будет удовлетворять заданной точности. Чтобы уменьшить время переходного процесса, на 1-м периоде [0, T] можно принять u(t) = at/T.
Реализация в SimInTech
Для построения частотной характеристики системы методом гармонического анализа в библиотеке блоков есть блок Harmonic Analyzer, который находится на вкладке «Анализ и оптимизация». Блок представляет собой субмодель, реализующую алгоритм прямого расчета частотной характеристики произвольной системы при подаче на вход синусоидального сигнала с дискретно изменяющейся частотой и заданной амплитудой колебаний.
Пример использования данного блока представлен в проекте, расположенном в директории установки SimInTech: SimInTech\Demo\Графики и исследования\Частотный анализ\Гармонический анализ\Динамическая система\Анализ динамической системы.prt
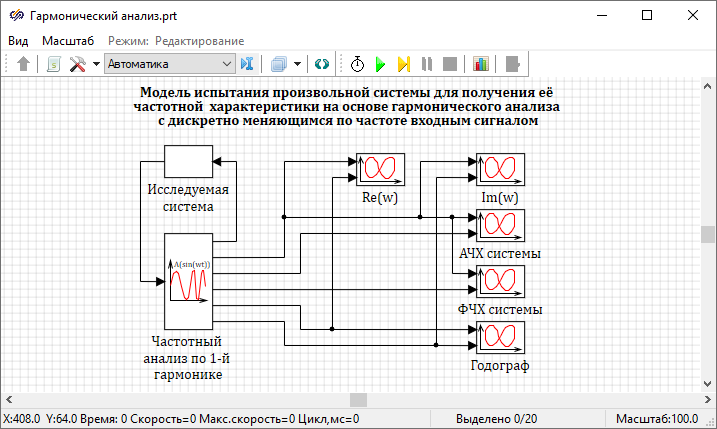
- Первый выход подключается ко входу исследуемой системы.
- Второй выход блока − значение круговой частоты исследуемой системы.
- Третий выход блока − значения АЧХ исследуемой системы.
- Четвертый выход блок − значения ФЧХ исследуемой системы.
- Пятый выход блока − значения действительной части АФЧХ исследуемой системы.
- Шестой выход блока − значения мнимой части АФЧХ исследуемой системы.
- Коэффициенты усиления k = 1.
- Постоянные времени T = 0.1.
- Коэффициент демпфирования b = 0.1.
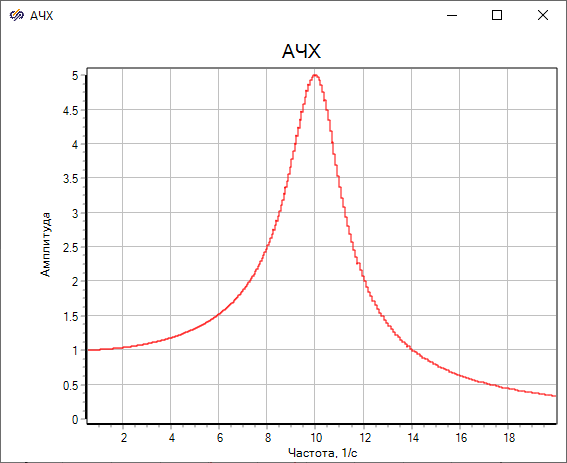
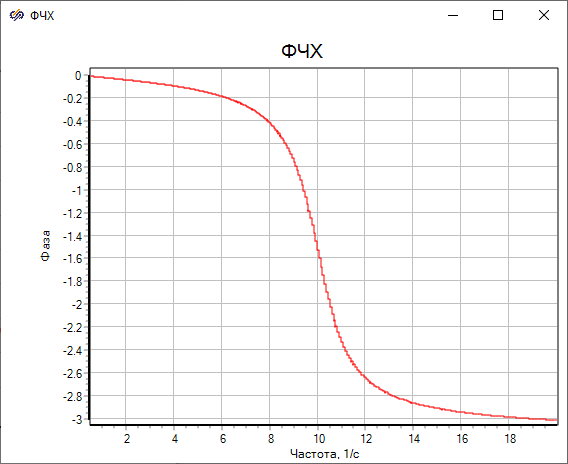
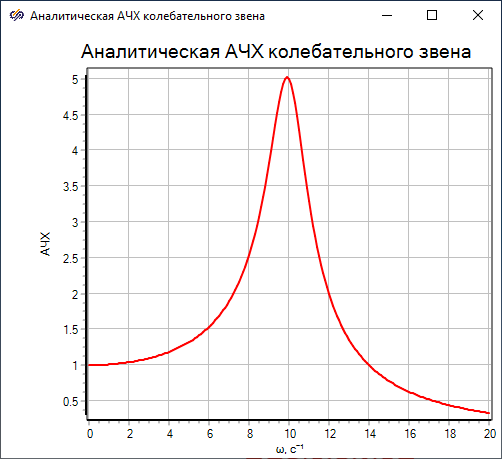
Данный метод пригоден для построения интегральной частотной характеристики произвольных нелинейных систем и позволяет оценивать АЧХ системы при разных амплитудах входного сигнала. К недостаткам данного метода относят иногда появляющуюся численную ошибку построенной АЧХ, которая уменьшается при увеличении количества интервалов, количества периодов стабилизации и при уменьшении частотного диапазона. Данный метод рекомендуется для построения АЧХ нелинейных систем, однако не позволяет получить информацию о генерации системой высших гармоник, поскольку оценивается только первая гармоника.
Спектральный анализ выходного сигнала системы методом подачи на вход системы шумоподобного сигнала или ступенчатого сигнала
Алгоритм спектрального анализа
Частотная характеристика системы оценивается и при подаче на вход системы шумоподобного (или иного сигнала с равномерной интегральной спектральной плотностью за заданный период времени) или же ступенчатого сигнала, и при построении спектральной плотности системы с использованием алгоритма быстрого преобразования Фурье (БПФ, FFT). В целом, алгоритм данного метода аналогичен алгоритму гармонического анализа, за исключением того, что оценивается не одна гармоника на одной дискретной частоте, а дискретный спектр частот, и на вход при этом подается не синусоидальный сигнал, а сигнал произвольного вида. С помощью данного метода получают информацию о генерации системой высших гармоник.
Реализация в SimInTech
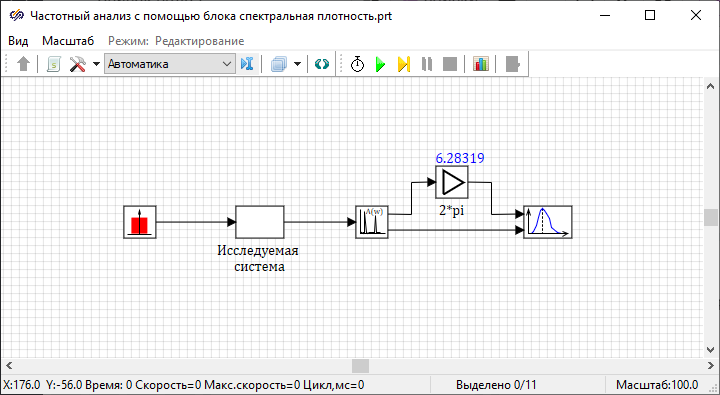
На вход исследуемой системы подается шумоподобный сигнал в диапазоне значений от −0.5 до 0.5 с математическим ожиданием 0 и размахом 1. На выходе системы подключен блок расчета спектральной характеристики, который оценивает спектр системы по выборке в 512 точек (настраивается в свойствах блока) с шагом 0.1 сек, с усреднением полученных спектров по всем сериям измерений. Выходной вектор частот умножается с помощью блока «Усилитель» на величину 2*pi для преобразования размерности частоты из [Гц] в [1/c].
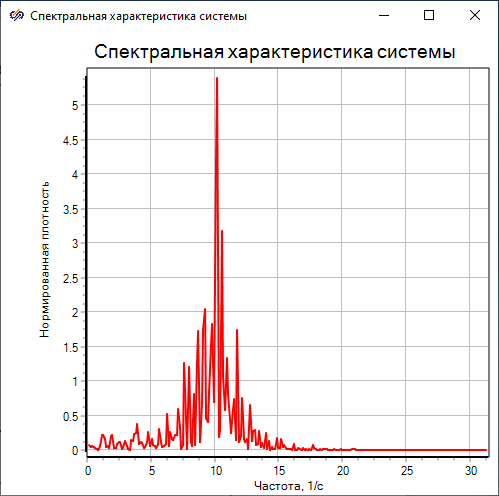
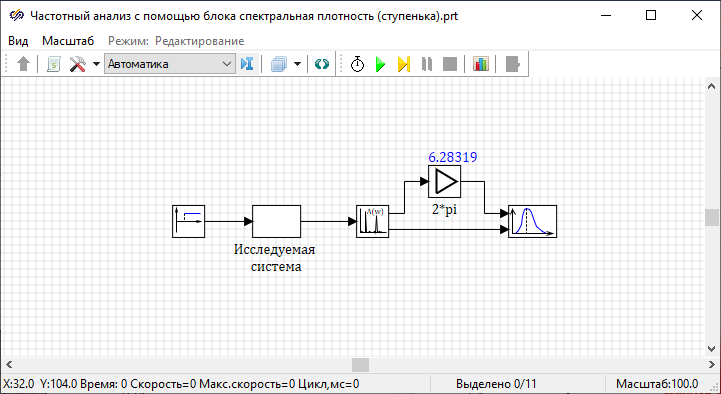
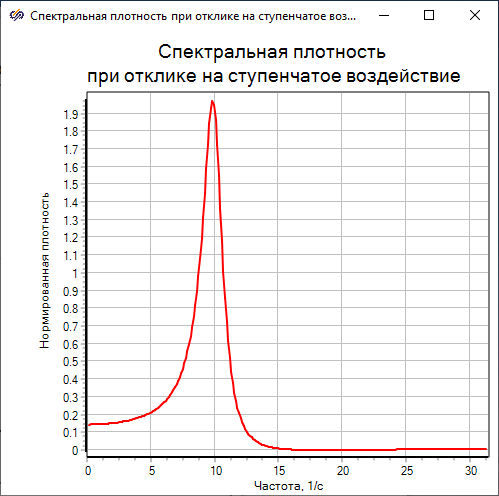
Преимущество данного метода – возможность оценки высокочастотных гармоник системы, недостаток – неоднозначность результата при анализе шумоподобного сигнала.
Заключение
Таким образом, для надежной оценки частотных характеристик нелинейных систем, имеющих в своих цепях релейные звенья и другие разрывные нелинейности, возможно использование метода гармонического анализа, а также измерения спектра отклика системы в ответ на ступенчатое входное воздействие.