Plotting of the root locus

		\| Vectorized \|
`in the palette`	`on the schematic`	\| Vectorized \|

The block is intended for plotting of the root locus, i.e. trajectories circumscribed in the complex plane by the poles (by characteristic polynomial roots) of a dynamical system when gain ratio is varying.

In this block, in order to find the roots of the dynamical system the calculation of transfer function opened system is employed. The function is following:

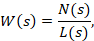
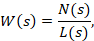
where N(s) and L(s) – characteristic polynomials of the system.

Based on the obtained transfer function of the system the characteristic polynomial is being formed that depends on the gain ratio, K:

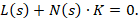
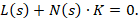
K value in i-th calculation point (i = 0 … N) is evaluated by the following formula:

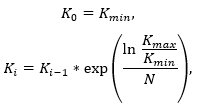
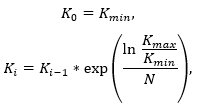
where K_min – initial set value of the gain ratio, K_max– final set value of the gain ratio, N – set number of output points.

Characteristic equation roots are found for each value of the gain ratio. The trajectories that circumscribed by the characteristic equation roots (i.e. root locus) are displayed in the complex plane. Double-click the block on the diagram to open the root locus plot.

Input Ports

Parameter	Description	Communication line type
in	Port for connection of the output signal of the object under study	Mathematical
out	Port for connection of the input signal of the object under study	Mathematical

Output Ports

The block has no output ports

Properties

Title	Parameter	Description	By default	Data type
Initial value of gain ratio K	kmin	Initial value of the opened system gain ratio range in which the characteristic polynomial roots will be found	0.1	Real
Final value of gain ratio K	kmax	Final value of the opened system gain ratio range in which the characteristic polynomial roots will be found	10	Real
Number of output points	ptcount	Number of the gain ratio values within the range for which the characteristic polynomial roots will be found (number of graph dots)	1000	Integer
Relative increment for Jackobian	dJotn	The value used for carrying out linearization of nonlinear objects	0.001	Real
Absolute increment for Jackobian	dJabs	The value used for carrying out linearization of nonlinear objects	1E-6	Real
Characteristics calculation mode	ffdcalcmode	It allows us to determine a moment of calculation: during schematic initialization, when the final calculation time is reached or with a preset step (i.e. "At the beginning of calculation", "At the end of calculation", "With a preset step")	At the beginning of calculation	Enumeration
Characteristics calculation step, sec	ffdtimestep	The time step value with that recalculation of characteristics goes on. This option is available when "With a preset step" characteristics calculation mode is selected	0	Real
Reduce degree of the numerator and the denominator polynomials	ReduceDeg	Checkbox to activate degree reducing of the numerator and the denominator polynomials	None	Binary
Absolute comparison accuracy of the roots of the numerator and the denominator when reducing degrees of polynomials	ReduceTol	Absolute allowable error in comparison of the roots of the numerator and the denominator when reducing degrees of polynomials. This option is available in the property "Reduce degree of the numerator and the denominator polynomials"	1E-5	Real

Прим.: property window is opened via context menu of the block

Parameters

Title	Parameter	Description	Data type
X values	X	Matrtix of the real numbers of the characteristic polynomial at each output point	Matrix
Y values	Y	Matrtix of the imaginary numbers of the characteristic polynomial at each output point	Matrix

Examples

Examples of block application: