SLE solving
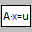 |
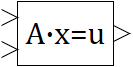 |
| Vectorized | |
in the palette |
on the schematic |
The block implements the procedure for solving a system of linear algebraic equations (SLE) of the form:
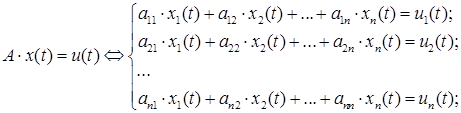
where A is the matrix of coefficients; x(t) is the solution vector; u(t) is the vector of the right-hand sides. The block has two vectorized input ports: 1st input port – for entering a matrix represented as a vector of coefficients when unpacking the matrix by rows. 2nd input port – for entering a vector (vector of the right parts). The block has one vector output port designed to output a vector (solution vector). The dimension of the vector signal on the 1st input port should be equal, where is the number of equations in the system, and the dimensions of the signals on the 2nd input port and on the output port are the same and equal.
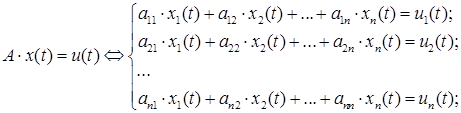
where A is the matrix of coefficients; x(t) is the solution vector; u(t) is the vector of the right-hand sides. The block has two vectorized input ports: 1st input port – for entering a matrix represented as a vector of coefficients when unpacking the matrix by rows. 2nd input port – for entering a vector (vector of the right parts). The block has one vector output port designed to output a vector (solution vector). The dimension of the vector signal on the 1st input port should be equal, where is the number of equations in the system, and the dimensions of the signals on the 2nd input port and on the output port are the same and equal.
Inputs
- matrix of coefficients is a port for entering a matrix represented as a vector of coefficients when unpacking the matrix by strings. The dimension of the vector signal on the 1st input port should be equal to n×n, where n is the number of equations in the system;
- right parts - a port for right parts vector input for the system. The dimension of the vector is n.
Outputs
- output - an output port of the solution vector. The dimension of the vector is n.
Properties
none
Parameters
none
Example
The following system of equations needs to be solved:
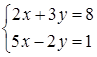
which has the obvious solution x=1, y=2. The figure below shows a structural diagram for solving this problem. Typical Multiplier blocks are used to generate input vector signals:

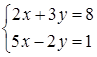
which has the obvious solution x=1, y=2. The figure below shows a structural diagram for solving this problem. Typical Multiplier blocks are used to generate input vector signals:

Note:
the block performs the procedure for solving the system of linear algebraic equations after each successful integration step.