Nonlinear translatory spring
 |
 |
| C | |
| in the palette | on the schematic |
The block is designed to simulate a nonlinear translatory spring with a constant spring constant.
The deformation (extension) of the spring s in m is determined by the formula:
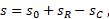
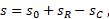
where:
- s0 – initial spring extension, m
- sC and sR – positions of bodies at ports "C" and "R", respectively, m
The dependence of the elastic force on the deformation value can be defined using a polynomial or a table.
Symmetric polynomial
This method allows you to define the dependence of the elastic force on the deformation value by a polynomial which is symmetric relative to zero:
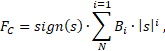
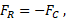
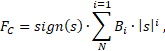
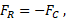
where:
- FC and FR – forces applied to ports "C" and "R", respectively, N
- Bi – i-th element of the vector of spring constants, N/m
- N – number of elements in the vector of spring constants
Asymmetric polynomial
This method allows you to define the dependence of the elastic force on the deformation value separately for extension and compression. The polynomial Bp defines the dependence at a positive deformation value (extension) and the polynomial Bn defines the dependence at a negative deformation value (compression):
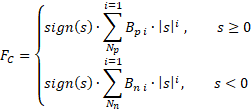
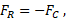
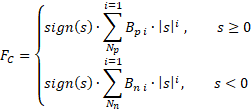
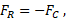
where:
- FC and FR – forces applied to ports "C" and "R", respectively, N
- Bpi – i-th element of the vector of spring constants Bp, N/m
- Bni – i-th element of the vector of spring constants Bn, N/m
- Np – number of elements in the vector of spring constants Bp
- Nn – number of elements in the vector of constants Bn
Table
This method makes it possible to calculate the elastic force depending on the deformation value by interpolating a given table. If the deformation value exceeds the specified vector of the deformation values, extrapolation is not carried out.
Inputs
| Name | Description | Connection line type |
|---|---|---|
| C | Port for connecting a conditionally fixed case (case) | Translatory mechanics |
| R | Port for connecting a conditionally movable rod (rod) | Translatory mechanics |
Outputs
None.
Properties
| Name | Parameter | Description | By default | Data type |
|---|---|---|---|---|
| Parameterization type | par_type | Allows you to specify the type of dependence of the elastic force on the deformation value. The possible values are: "Polynomial", "Table" | Polynomial | Перечисление |
| Symmetry | sym_type | Allows you to define a polynomial that is symmetric with respect to zero. The property is available when you select the "Polynomial" parameterization type. The possible values are: "Yes", "No" | Yes | Двоичное |
| Vector of spring constants, N/m | B | Vector of spring constants. The property is available when the "Polynomial" parameterization type is selected and the "Symmetry" property is enabled | [100 , 0 , 10 , 0 , 1] | Массив |
| Vector of spring constants for S ≥ 0, N/m | Bp | Vector of spring constants at positive deformation (extension). The property is available when the "Polynomial" parameterization type is selected and the "Symmetry" property is disabled | [100 , 0 , 10 , 0 , 1] | Массив |
| Vector of spring constants for S < 0, N/m | Bn | Vector of spring constants at negative deformation (compression). The property is available when the "Polynomial" parameterization type is selected and the "Symmetry" property is disabled | [1000 , -10 , 100 , 0 , 0] | Массив |
| Vector of deformation values, m | Sx | Vector of deformation values. The property is available when you select the "Polynomial" parameterization type. | [-1 , -0.5 , -0.3 , -0.1 , 0.1 , 0.3 , 0.5 , 1] | Массив |
| Vector of elastic forces, N | Fy | Vector of spring elastic forces, N The property is available when you select the "Polynomial" parameterization type. | [-1000 , -400 , -200 , -50 , 50 , 200 , 400 , 1000] | Массив |
| Initial extension (Sr - Sc), m | S0 | The initial extension of the spring at the zero positions of the bodies on the ports of the block. A negative value sets the pre-compression | 0 | Вещественное |
Parameters
| Name | Parameter | Description | Data type |
|---|---|---|---|
| Spring deformation, m | S | Extension value. Negative values mean compression | Вещественное |
| Elastic force, N | F | Force transmitted to port "R" | Вещественное |
Examples
Examples of block application: