Analytical aperiodics of the 1st order
 |
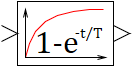 |
| Vectorized | C | |
in the palette |
on the schematic |
The block implements an analytic-discrete mathematical model of the aperiodic link of the 1st order, the continuous mathematical model of the dynamics of which is described by a linear ordinary differential equation (ODE) of the form:
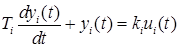
where ui(t) is the i-th element of the input signal to the block, Ti is an element of the time constant vector, ki is an element of the gain vector, yi(t) is an element of the output signal from the block. Mandatory requirement Ti≠0
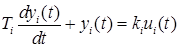
where ui(t) is the i-th element of the input signal to the block, Ti is an element of the time constant vector, ki is an element of the gain vector, yi(t) is an element of the output signal from the block. Mandatory requirement Ti≠0
The block algorithm implements the calculation of the output signal at discrete moments of time (at each step of integration, including the bad steps) according to the following ratio:
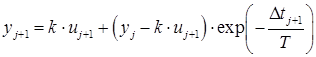
where yi is the value of the signal at the input and output of the block at the j-th step of integration, xj+1 is the value of the signal at the input of the block at the (j+1)-th step of integration, ∆tj+1 is the current step of integration.
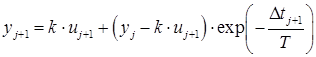
where yi is the value of the signal at the input and output of the block at the j-th step of integration, xj+1 is the value of the signal at the input of the block at the (j+1)-th step of integration, ∆tj+1 is the current step of integration.
Inputs
- input - input signal.
Outputs
- output - output converted signal.
Properties
- Gain coefficients – vector of coefficients ki, by which the input value is multiplied;
- Time constants – vector of time constants Ti in seconds;
- Initial conditions – vector of initial values yi(0) of the block output quantity;
- Auxiliary inputs – indicates the presence of additional inputs of the block;
- The initial conditions are taken from – the source pointer of the initial conditions of the block.
Parameters
None