Inertia-integrating link
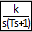 |
 |
| Vector | C | ST | |
| in the palette | on the schematic |
The block is vectorized. It implements the mathematical model of the link, the dynamics of which is described by a linear ordinary differential equation (ODE) of the following form:
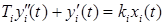
where xi(t) is the i-th element of the input signal to the block, Ti is an element of the time constant vector, ki is an element of the gain vector, yi(t) is an element of the output signal from the block. Under zero initial conditions, the dynamics of the block can be represented by the following transfer function:
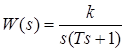
therefore, the icon of this block has the form of the transfer function of the inertia-integrating link. The dimensions of the input signal, output signal and coefficient vector must match. Mandatory сondition: Ti≠0.
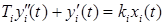
where xi(t) is the i-th element of the input signal to the block, Ti is an element of the time constant vector, ki is an element of the gain vector, yi(t) is an element of the output signal from the block. Under zero initial conditions, the dynamics of the block can be represented by the following transfer function:
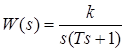
therefore, the icon of this block has the form of the transfer function of the inertia-integrating link. The dimensions of the input signal, output signal and coefficient vector must match. Mandatory сondition: Ti≠0.
Inputs
- input - input signal.
Outputs
- output - output converted signal.
Properties
- Gain coefficients – vector of coefficients ki, by which the input value is multiplied;
- Time constants – vector of time constants Ti in seconds;
- Initial conditions – vector of initial values yi of the block output value;
- Initial conditions for the derivative – the vector of the initial conditions for the derivative of the output quantity yi`(0) of the block.
Parameters
- Dynamic variables - internal block condition variables;
- Derivatives - internal block condition variables.
Note:
by default, the block parameters are set for the scalar input signal.