Rotary friction
 |
 |
| C | |
| in the palette | on the schematic |
The block is designed to simulate the contact friction of two rotating surfaces with a constant pressing force.
The relative slip speed ω in rad/s is determined by the formula:
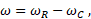
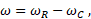
where ωC, ωR – angular speeds at ports "C" and "R", respectively, rad/s
The Stribeck curve [1] and viscous friction (Figure 1) are used to determine the friction torque.
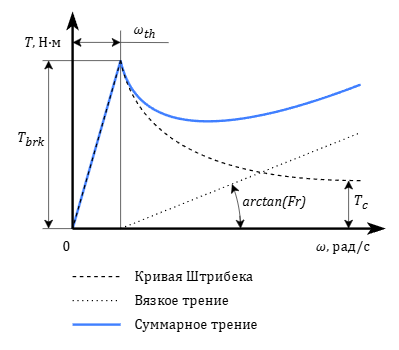
Figure 1. Dependence of friction torque on relative speed

The friction torque is determined by the formula:
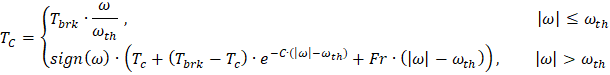
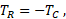
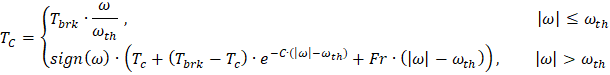
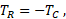
where:
- TC and TC – torques applied to ports "C" and "R", respectively, Nm
- Tbrk – breakaway friction torque, Nm
- Tc – dry (coulomb) friction torque, Nm
- ωth – breakaway angular speed, rad/s
- C – damp ratio, s/rad
- Fr – coefficient of internal friction, Nm·s/rad
The value of the breakaway friction torque Tbrk in Nm is displayed next to the block.
Inputs
| Name | Description | Connection line type |
|---|---|---|
| C | Port for connecting a conditionally fixed case (case) | Rotary mechanics |
| R | Port for connecting a conditionally moving shaft (rotor) | Rotary mechanics |
Outputs
None.
Properties
| Name | Parameter | Description | By default | Data type |
|---|---|---|---|---|
| Breakaway friction torque, Nm | Tbrk | Breakaway friction torque | 2 | Вещественное |
| Breakaway angular speed, rad/s | Wth | The threshold value of the speed below which the value of the friction torque is reduced to achieve the stability of the numerical solution | 0.001 | Вещественное |
| Dry (coulomb) friction torque, Nm | Tc | Dry (coulomb) friction torque | 1 | Вещественное |
| Damp ratio, s/rad | C | Damp ratio | 1 | Вещественное |
| Coefficient of internal friction, Nm·s/rad | Fr | Coefficient of internal friction | 0.1 | Вещественное |
Parameters
| Name | Parameter | Description | Data type |
|---|---|---|---|
| Angular speed differential, rad/s | W | Relative slip speed | Вещественное |
| Friction torque, Nm | T | Torque at the port "R" | Вещественное |
| Power of friction torque, W | Q | Power of friction torque, W | Вещественное |
Examples
Examples of block application:
Literature
- Richard Stribeck: Die wesentlichen Eigenschaften der Gleit- und Rollenlager, Z. Verein. Deut. Ing. Vol. 46 Seite 38ff. 1341–1348 (1902).